Peut-on savoir ce que l’on ne sait pas ? La quantification d’incertitude pour accéder au risque (presque) zéro

27 Juin 2023A la une, Qualification de la confiance

 Les méthodes de quantification d’incertitude dans les codes de calcul classiques sont fiables et robustes mais deviennent un défi important quand il s’agit d’intelligence artificielle ; on vous dit tout dans cet article.

 

Qu’est-ce que la quantification d’incertitude et quel est son impact ?

“Tous les modèles sont faux, mais certains sont utiles” : telle est la conclusion du statisticien britannique George Box en 1976. Si la citation est volontairement provocatrice, elle n’en est pas moins vraie. En effet, les modèles que nous utilisons pour comprendre le monde et prédire divers phénomènes ne sont pas parfaitement précis. Ils sont généralement des simplifications de la réalité et comportent des incertitudes. 

Même en n’étant pas exacts, les modèles basés sur l’Intelligence Artificielle (IA) trouvent leurs utilités dans différents domaines comme l’ingénierie, la physique ou la médecine en fournissant une base de connaissances et d’aides à la décision. Cependant, l’utilisation de l’IA comporte toujours des risques liés à l’incertitude et peut parfois engendrer des erreurs aux conséquences lourdes.  

Par exemple, dans le domaine des véhicules autonomes, une incertitude excessive dans la reconnaissance des objets sur la route peut entraîner des accidents et mettre en danger des vies humaines. Dès lors, comment peut-on quantifier les incertitudes et conclure sur la fiabilité des systèmes basés IA ? 

 

Les sources d’incertitudes et leurs types

Généralement, on distingue deux sources d’incertitudes : l’incertitude épistémique et l’incertitude aléatoire. L’incertitude épistémique fait référence à l’incertitude due à notre connaissance limitée ou imparfaite d’un système ou d’un phénomène. Elle se produit lorsque nous manquons d’informations précises, fiables ou complètes pour prendre des décisions ou faire des prédictions exactes. Prenons le modèle linéaire (ligne droite) illustré dans la figure ci-dessous. Celui-ci représenterait par exemple le lien entre les heures de révisions et la note à l’examen de plusieurs étudiants au lycée. En moyenne, le modèle réussi à capturer la corrélation positive : plus le temps de révision est grand, meilleure est la note. Cependant, cette association n’est pas prédite de manière parfaite (l’écart entre la réalité et le modèle est illustré par le segment rouge).  

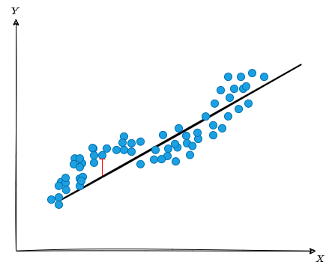
Figure 1 : Illustration d’un modèle linéaire entraîné sur un jeu de données

L’incertitude épistémique peut être réduite par l’acquisition de nouvelles connaissances, de données supplémentaires ou de meilleures méthodes d’analyse. Ainsi, en récoltant plus de données et en augmentant la complexité du modèle d’IA, on peut alors espérer réduire l’erreur de prédiction comme le montre la figure qui suit (concentration du nuage de points autour des prédictions).

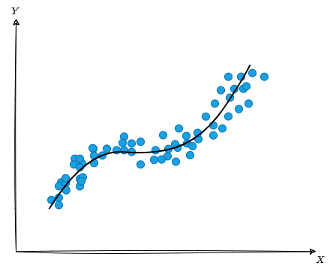
Figure 2 : Illustration d’un modèle Machine Learning plus représentatif, entraîné sur le même jeu de données que la Figure 1

L’incertitude aléatoire, quant à elle, est liée à la variabilité intrinsèque d’un phénomène ou d’un système : elle est irréductible. Elle est due à des facteurs imprévisibles et incontrôlables gouvernés par le hasard. Contrairement à l’incertitude épistémique, l’incertitude aléatoire ne peut pas être complètement atténuée, mais elle peut être quantifiée et gérée en utilisant des approches statistiques appropriées. Dans l’exemple précédent, même avec une connaissance approfondie des étudiants et des modèles complexes, il restera toujours une part de hasard non-modélisable : aucun modèle d’IA ne sera jamais capable de prédire sans erreur la note d’un élève. 

Les incertitudes proviennent de sources différentes : mesures de capteurs bruitées, données manquantes, algorithmes inexacts, etc. Comprendre l’origine des incertitudes et quantifier leurs impacts sont essentiels pour concevoir une IA fiable et robuste, particulièrement en évaluant les risques associés à son utilisation au sein de systèmes critiques dans les domaines du transport, de la santé et de la défense. 

 

Les techniques de quantification d’incertitude

Dans le domaine de l’apprentissage automatique, la quantification d’incertitude peut être utilisée sous de multiples formes : un intervalle de valeurs vraisemblables (ensembles de prédictions), la connaissance de la probabilité de faire le bon choix (classification calibrée), ou encore la possibilité de s’abstenir de prendre une décision lorsque notre modèle n’est pas sûr (prédiction sélective). Ces formes sont liées au type de problème que nous voulons résoudre : régression (par ex., prévision de consommation d’énergie), classification (piéton ou véhicule), etc.  

On retrouve alors les notions d’incertitude aléatoire et épistémique. D’une part il faut correctement modéliser la variabilité intrinsèque du phénomène décrit. D’autre part, il faut tenir compte de l’erreur induite par une modélisation imparfaite. Pour chacune de ces sources d’incertitude, deux familles d’approche se concurrencent : celle basée sur les “probabilités”, et celles basées sur les “ensembles de modèles”.  Dans les deux cas, la finalité se traduit souvent au travers de la tolérance aux risques d’erreurs de la part du système, formulée par exemple comme : “nous ne voulons pas manquer la vraie cible plus de 5% du temps ».  

Caractériser l’incertitude épistémique nécessite de prendre en compte le nombre limité d’observations à notre disposition pour ajuster au mieux le modèle prédictif. Pour ce faire, une première approche consiste à estimer l’erreur de prédiction du modèle afin de corriger ses prédictions. Une autre approche, dénommée bayésienne, vise à modéliser l’information issue des observations combinée à la connaissance a priori du phénomène étudié. Une troisième approche consiste à capturer l’incertitude au travers d’un métamodèle basé sur un ensemble de sous modèles ayant une bonne diversité. Le « bon » choix se résume aux besoins opérationnels des utilisateurs et à leur solution de ML existante : certaines approches sont utilisables post-hoc (par ex., prédiction conforme [1]), d’autres nécessitent de définir la connaissance a priori avec un modèle prédictif dédié, tel que les réseaux de neurones bayésiens [2], ou de manipuler un métamodèle agrégant un ensemble diversifié de sous modèles. 

 

La quantification d’incertitude sur des cas d’usage au sein de Confiance.ai

Au sein de Confiance.ai, plusieurs équipes ont travaillé sur le sujet, notamment la quantification d’incertitude liée à la prédiction de la demande de gaz pour Air Liquide : les données couvrent l’historique de la demande de plusieurs types de livraisons de gaz, ainsi que des informations de type contextuel. Des approches mentionnées précédemment, nous en mentionnons deux : la première méthode [1] fait le post-processing du modèle prédictif en production chez Air Liquide avec de la prédiction conforme et la deuxième [2] consiste à entraîner des réseaux bayésiens. 

La figure ci-dessous représente la prédiction de la demande de différentes livraisons de produits fournis par Air Liquide, en sachant qu’une livraison se définit par une combinaison d’une source de production de gaz, d’un type de gaz produit, et d’une zone de distribution. Il est intéressant de constater qu’on observe une forte variabilité des incertitudes en fonction du type de livraison réalisée. Certaines prédictions sont très incertaines (intervalle bleu plus large), d’autres sont au contraire plus sûres (intervalle bleu plus étroit).

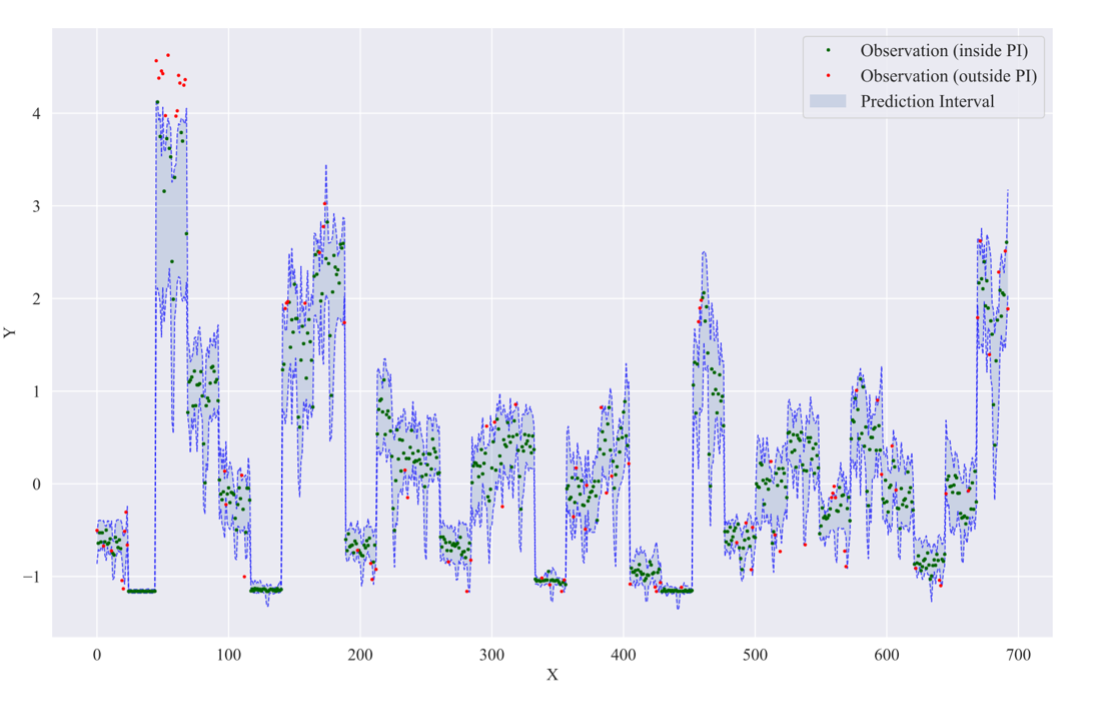
Figure 3a : « Cas d’usage Air Liquide : quantification de l’incertitude d’un modèle ML appliqué au série temporelles ».

Figure 3b : « Cas d’usage Air Liquide : quantification de l’incertitude d’un modèle ML appliqué au série temporelles ».

Un algorithme de prédiction conforme avec un niveau de confiance de 90%, appliqué au cas d’usage d’Air Liquide. Les bandes bleues quantifient l’incertitude autour de la prédiction ponctuelle (en noire) ; approximativement 90% des cibles (points verts) sont incluses dans l’intervalle de prédiction et les 10% restantes (points rouges) sont en dehors de l’intervalle.

En s’appuyant sur des données, les méthodes de quantifications d’incertitude permettent d’associer un intervalle de confiance aux prédictions d’un modèle d’apprentissage. Ce résultat doit alors être confronté aux besoins des utilisateurs de ces prédictions afin d’adapter la prise de décision en présence de fortes incertitudes. On s’aperçoit de la criticité d’avoir une incertitude bien “quantifiée” pour un modèle ML donné : si on intègre un tel composant dans un environnement industriel, la chaine décisionnelle qui mène aux différents choix de planification de la production jusqu’à la distribution, pourra en bénéficier en adaptant les niveaux d’approvisionnement et de  production, la gestion du personnel et de la distribution, etc. 

 

La quantification d’incertitude est incontournable pour la mise en œuvre de solutions ML fiables. Les sources d’incertitude sont multiples et il existe plusieurs approches pour en mesurer l’impact. A ce titre, Confiance.ai contribue activement à cette thématique dans un environnement de recherche et d’industrie d’excellence, notamment à travers de publications scientifiques et de transferts technologiques. Dans la course à l’IA de confiance, les industriels qui maitriseront ce sujet auront nettement un pas d’avance. 

 

Un article rédigé par Luca Mossina (IRT Saint-Exupéry), Mouhcine Mendil, (IRT Saint-Exupéry), Eiji Kawasaki (CEA), Kevin Pasini (IRT SystemX) et Marc Nabhan (Air Liquide).

 

Bibliographie et outils

Des résultats issus du programme Confiance.ai :